Cosinus et Sinus : Une Exploration Mathématique

Mariam Ait Merri

• avril 22, 2024

Au cœur même des mathématiques se trouvent des concepts aussi intrigants que le cosinus et le sinus. Ces deux fonctions qui défient l’intuition et captivent l’imagination. Leurs noms évoquent des images de triangles, de cercles et d’ondes. Mais leur importance va bien au-delà de ces simples représentations géométriques. Ces fonctions trigonométriques, bien qu’on les perçois comme abstraites, sont en réalité des piliers fondamentaux de la discipline mathématique. Et leur influence s’étend à de nombreux domaines, de la physique à l’ingénierie en passant par la musique et l’art.

Dans cette exploration approfondie, nous plongerons dans les méandres du cosinus et du sinus. Dévoilant leurs origines géométriques. Et explorant leurs propriétés fascinantes et démontrant leurs applications pratiques dans le monde réel. Préparez-vous à être guidé à travers un voyage mathématique riche en découvertes. Où la symétrie, la régularité et la beauté se rejoignent dans une danse infinie de formules et de théorèmes. Bienvenue dans notre exploration approfondie du cosinus et du sinus. Où chaque équation cache un trésor de sens et chaque courbe révèle un nouvel aspect de l’univers mathématique.

Les Origines Antiques de la Trigonométrie : Fondements Géométriques et Astronomiques du Cosinus et du Sinus

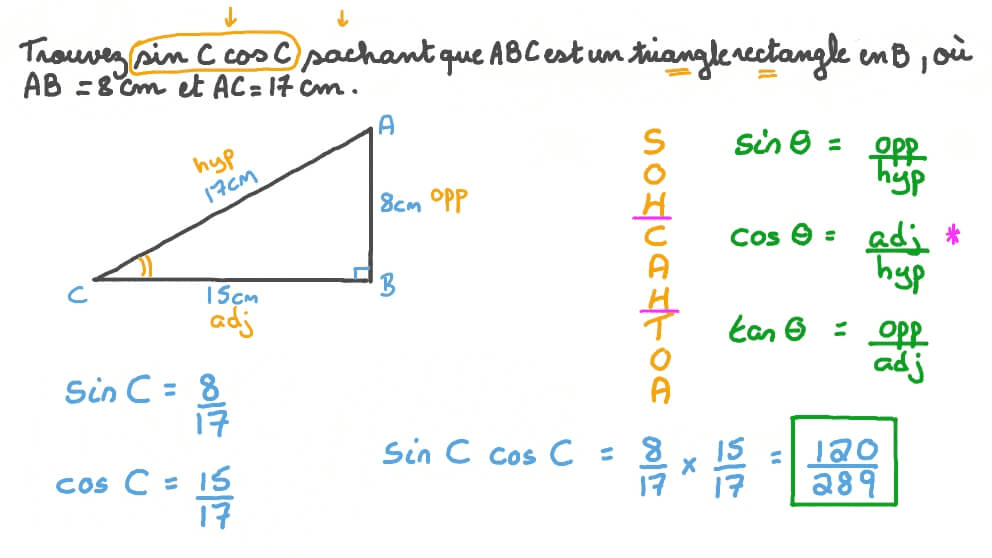
Pour remonter aux sources du cosinus et du sinus, il est nécessaire de plonger dans les profondeurs de la géométrie ancienne. Ces fonctions tirent leur essence même des relations fondamentales qui existent entre les côtés et les angles des triangles. Dans un triangle rectangle, où l’un des angles mesure 90°, le cosinus d’un angle aigu est défini comme le rapport de la longueur du côté adjacent à cet angle sur l’hypoténuse. Tandis que le sinus est défini comme le rapport de la longueur du côté opposé à cet angle sur l’hypoténuse.

Cette notion simple découle directement de la définition de ces fonctions trigonométriques à partir des proportions des côtés d’un triangle. Et c’est une idée qui remonte aux mathématiciens de l’Antiquité, tels que les Babyloniens et les Grecs. Les mathématiciens grecs, en particulier, ont développé des outils géométriques pour étudier les relations entre les angles et les côtés des triangles. Jetant ainsi les bases de la trigonométrie moderne.

Cependant

Le développement de ces concepts trigonométriques ne s’est pas limité à la géométrie des triangles. Les premières traces de trigonométrie remontent à des civilisations anciennes qui utilisaient des connaissances astronomiques. Et ce pour comprendre les mouvements célestes. Les Égyptiens, les Babyloniens et les Indiens ont tous contribué à l’étude des angles et des cycles périodiques. Jetant ainsi les bases de ce que nous appelons aujourd’hui la trigonométrie. Par exemple, les astronomes babyloniens ont utilisé des tables de valeurs trigonométriques pour calculer les mouvements des planètes et des étoiles. Démontrant ainsi l’importance pratique de ces concepts pour la navigation et l’astronomie.

Ainsi, les origines du cosinus et du sinus sont profondément enracinées dans l’histoire des mathématiques et de la science. Depuis les premières explorations géométriques des anciens jusqu’aux développements astronomiques des civilisations antiques. Et ces fonctions trigonométriques ne sont pas seulement des outils mathématiques abstraits. Mais aussi des instruments puissants pour comprendre les relations entre les formes, les mouvements et les phénomènes périodiques qui sous-tendent notre univers.

Exploration des Propriétés Envoûtantes du Cosinus et du Sinus

Les propriétés du cosinus et du sinus offrent un terrain fertile pour l’exploration mathématique. Au-delà de leur définition géométrique initiale, ces fonctions trigonométriques révèlent une richesse de caractéristiques fascinantes :

Ces propriétés, parmi d’autres, font du cosinus et du sinus des outils essentiels dans la modélisation, l’analyse et la résolution de problèmes dans divers domaines mathématiques et scientifiques.

Contenu similaire

• Fonction Exponentielle : Fondements et Applications
• ‘Les Fleurs du Mal’ : Éclats de Beauté dans les Ténèbres
• ‘Le Malade Imaginaire’ : Univers hilarant et intemporel de Molière

Applications Pratiques dans la Science, l’Ingénierie, et l’Art

En physique, les fonctions trigonométriques trouvent une utilisation étendue dans la modélisation des phénomènes périodiques. Par exemple elles permettent les oscillations harmoniques, les ondes sonores et les mouvements vibratoires. Et ces fonctions sont aussi indispensables pour comprendre le comportement dynamique des systèmes physiques. Comme les pendules simples, les systèmes ressort-masse et les vibrations mécaniques.

Dans le domaine de l’ingénierie, le cosinus et le sinus sont des outils incontournables pour la modélisation et le contrôle des systèmes dynamiques. Des applications variées telles que la conception de circuits électriques. Ou encore le contrôle des robots, la navigation par satellite et la stabilisation des systèmes mécaniques font appel à ces fonctions pour représenter et réguler les mouvements et les processus.

Les sciences naturelles font également un large usage des fonctions trigonométriques pour analyser et prédire des phénomènes périodiques observés dans la nature. Des domaines tels que l’océanographie, la météorologie et la biologie utilisent le cosinus et le sinus pour étudier les marées, les variations climatiques et les cycles biologiques. Fournissant ainsi des informations cruciales sur les modèles et les tendances dans notre environnement.

Mais encore !

En traitement du signal, le cosinus et le sinus sont au cœur de nombreuses techniques d’analyse et de synthèse de signaux. Ils sont utilisés pour décomposer des signaux complexes en composantes périodiques. Pour compresser des données audio et pour détecter des motifs dans les séries temporelles. Contribuant ainsi à une meilleure compréhension et à une meilleure manipulation des signaux électriques et acoustiques.

Enfin, dans le domaine de la musique et de l’art, les fonctions trigonométriques sont omniprésentes. Elles sont utilisées pour comprendre la théorie musicale. Ou aussi générer des sons dans les synthétiseurs électroniques, créer des motifs visuels basés sur des formes périodiques. Et bien plus encore, offrant ainsi un langage mathématique riche pour l’expression artistique et créative.

Conclusion

En conclusion, l’exploration des fonctions cosinus et sinus nous a révélé la profondeur et la pertinence des concepts mathématiques dans notre monde moderne. Du géométrique à l’applicatif, ces fonctions jouent un rôle crucial dans de nombreux domaines, de la physique à l’ingénierie en passant par l’art et la musique.

Si vous souhaitez approfondir vos connaissances en mathématiques ou explorer d’autres domaines des sciences, trouver un professeur compétent peut faire toute la différence. SmartProf offre une plateforme efficace pour trouver des professeurs de maths qualifiés qui peuvent vous guider dans votre apprentissage. Avec leur expertise et leur passion, ils peuvent vous aider à maîtriser les concepts du cosinus, du sinus et bien plus encore. Vous permettant ainsi de réaliser vos objectifs académiques et professionnels. Explorez SmartProf dès aujourd’hui pour découvrir comment vous pouvez transformer votre compréhension des mathématiques et ouvrir de nouvelles perspectives passionnantes.